Символьный ИИ обозначает совокупность методов, в которых знания представляются в виде символов и их отношений, то есть в виде некоторого формального языка. Символьный ИИ основан на способности человека понимать мир путем формирования символьных представлений и их взаимосвязей и создавать правила для фиксации знаний. Способность общаться с помощью символов – одно из проявлений нашего интеллекта. Символы играют ключевую роль в процессе мышления и рассуждения человека.
С помощью символов мы можем представлять окружающие нас предметы (машина, кошка, собака). Это могут быть не только перечисленные материальные объекты, но и абстрактные понятия (демократия, капитализм, транзакция). Символы могут быть организованы в иерархию (автомобиль состоит из дверей, окон, шин, сидений и т. д.). Символы могут использоваться для описания других символов (красное яблоко, тяжелый груз). Способность человека манипулировать символами существовала тысячи лет до появления термина “искусственный интеллект”.
С помощью символов могут быть построены логические конструкции (если Петя является сыном моей дочери, то, следовательно, Петя мой внук). Символьный искусственный интеллект также иногда именуют как “Rule based AI” – ИИ, основанный на правилах. В некоторых публикациях в качестве синонима понятия “символьный ИИ” используют сокращение GOFAI (“Good Old-Fashioned Artificial Intelligence” – “старый добрый искусственный интеллект”), по имени, которое использовал Джон Хоугеланд в своего курса “Искусственный интеллект: Основная идея”.
Для обозначения альтернативных подходов, не использующих явно символы высокого уровня, используют термин “субсимвольный ИИ”.
Приведем простой пример применения подходов символьного ИИ на практике: пусть некая скоринговая программа использует символьные переменные “пол”, “возраст”, “профессия” и т. п., которые могут принимать определенные значения. В программе заданы правила типа “Если профессия “программист”, пол мужской, а возраст попадает в промежуток от 30 до 40 лет, то некоторая переменная, участвующая в определении кредитного рейтинга, примет такое-то значение”. При этом очевидно, что логика, по которой оценивается кредитный рейтинг респондента в данном примере задана изначально, вычисляется она по определенным правилам, может быть явно прочитана человеком, а подобного рода вывод программы является объяснимым. Определив совокупность правил вышеуказанным способом и задавая на входе совокупность параметров, по которым мы оцениваем потенциальных клиентов, можно решать такие задачи, как оценка целесообразности выдачи кредита.
Говорят, что символьный ИИ относится к объяснимым (или интерпретируемым) методам ИИ, поскольку позволяет рассуждать о том, каким образом получен достигнутый результат.
В рамках символьного подхода мы можем определить некоторую сущность набором признаков и связей. Например, яблоко-это фрукт, который растет на дереве, яблоко может быть красного, желтого или зеленого цвета и так далее (рис. 1.17).
Рис. 1.17. Набор признаков и связей, определяющих понятие “яблоко” в символьном подходе. Источник: Marvin Minsky
Определив набор сущностей, выраженных в виде символов и отношений между ними, мы приходим к понятию ” семантические сети” – сети, которые представляют собой направленный граф, вершины которого соответствуют объектам, а дуги (линии) – отношениям между ними.
Достоинство семантических сетей состоит в том, что это человеко-читаемый наглядный способ представления знаний.
Примером семантической сети является граф, отражающий взаимодействия в семейной системе, где на основе указанных связей можно получить характер родственных отношений между всеми членами группы (рис. 1.18).
Рис. 1.18. Граф, отражающий взаимодействия в семейной системе
Используя в качестве семантической сети (базы знаний) семейное дерево, то есть зная имена и родственные связи и следуя цепочке рассуждений типа “Если Анна мать Елены, а Елена мать Евгения, то Евгений – это внук Анны”, система может генерировать ответы на вопросы о родственных отношениях всех участников системы.
Используя базу знаний, представляющую собой набор фактов, правил и отношений, символьная ИИ-система позволяет вести рассуждения, основанные на алгебраическом манипулировании имеющимися знаниями и отвечать на вопросы. Понятный человеку процесс получения выводов в символьных моделях облегчает контроль в их построении и отладке.
При этом отметим, что символьная система ИИ, по крайней мере в классическом ее понимании, не может обучаться сама, она опирается на базы знаний, которые явно закладываются в систему разработчиком.
Эффективность такой системы зависит от объема и качества базы знаний. Если система получает запрос, по которому знания либо отсутствуют, либо ошибочны, система не сможет дать удовлетворительный ответ.
Приведенный пример на рис. 1.18 ограничен набором людей, связанных заранее известными (родственными) отношениями, однако если попытаться построить граф взаимоотношений из случайного набора людей, задача окажется намного сложнее.
С точки зрения области применения, следует отметить, что символьный подход лучше всего работает в задачах с четко определенными правилами. Например, символьный подход показал хорошие результаты в доказательстве теорем, в программах для игры в шахматы.
В частности, символьный подход (наряду с другими методами) был использован в решении Deep Blue, победившем чемпиона по шахматам Каспарова в 1997 году.
Символьные подходы были доминирующей парадигмой исследований в области ИИ с середины 1950-х до середины 1990-х, они показали свою эффективность в задачах с четко заданными правилами, однако открытые системы, такие как задачи на ориентацию в “обыденной реальности мира”, слишком беспорядочны, чтобы представлять их в виде универсально обоснованных правил логики, которыми оперирует символьный ИИ.
Символьный подход в основном ориентирован на извлечение знаний из экспертов, однако существуют методы, извлекающие знания из данных. Примером такого подхода является алгоритм дерева решений – метод обучения с учителем. Цель алгоритма – создать дерево правил, которые можно использовать для прогнозирования выходных данных при заданных входных данных. Дерево решений – это тип направленного ациклического графа, который отображает решения и их последствия. Логика дерева решений наглядно представляется графом и понятна человеку. Деревья решений могут работать как с дискретными, так и с непрерывными переменными, их можно использовать для задач регрессии и классификации, речь о которых пойдет далее в этой лекции.
Дерево решений обычно начинается с одного узла, который разветвляется на возможные результаты. Каждый из этих результатов приводит к дополнительным узлам, которые разветвляются на другие возможности, что и позволяет говорить о древовидной структуре.
Пример дерева решений показан на рис. 1.19. Начиная с отправной точки “могу ли я начать писать статью”, решения принимаются в зависимости от последовательности ответов на вопросы, каждый из которых зависит от результатов предыдущих ответов. Так двигаясь по той или иной ветке дерева, мы достигаем результата.
Дерево решений – это простейший способ извлечения знаний из данных, существуют и другие. Такой подход изучается в рамках направления интеллектуального анализа данных (Data Mining) или “добычи знаний из баз данных” (Knowledge Discovery in Databases).
Рис. 1.19. Дерево решений
В первую очередь символьный ИИ ассоциируется с экспертными системами и базами знаний.
Экспертные системы были одними из первых действительно успешных форм программного обеспечения для ИИ. Экспертная система эмулирует способность человека-эксперта по принятию решений путем рассуждений на основе совокупности знаний, представленных в виде правил. Первые экспертные системы были созданы в 1970-х годах. К наиболее ранним примерам можно отнести программу MYCIN, которая была разработана в 1972 году и диагностировала инфекционные заболевания крови.
Другой пример – система PROSPECTOR, созданная в 1974-83 гг. для геологических изысканий.
Так же, как и MYCIN, PROSPECTOR вовлекает геолога в диалог, с тем чтобы, опираясь на его наблюдения в качестве источника исходных данных, выбрать модель и дать ответ на вопросы “Где бурить?” и “Где искать?”. В 1984 г. система достаточно точно предсказала существование месторождения молибдена, оцененного в многомиллионную сумму.
Широкое распространение экспертные системы получили в 1980-х годах. В 1980 году для корпорации Digital Equipment Сorp. была создана экспертная система под названием XCON, которая, по свидетельству разработчиков, экономила до 40 млн долларов ежегодно. С начала 1980-х годов корпорации по всему миру начали разрабатывать экспертные системы. Можно сказать, что выход из очередной зимы искусственного интеллекта в 1980-х годах произошел именно на волне разработок ИИ в форме экспертных систем. Основные элементы экспертной системы показаны на рис. 1.20.
Как видно из рисунка, одним из ключевых элементов системы является инженер по знаниям, который должен выудить из эксперта (и формализовать) тот набор знаний, которым этот специалист владеет. Иногда это является нетривиальной задачей, что связано не только с нежеланием некоторых экспертов делиться всеми знаниями, но и со сложностью вербализации и формализации некоторых знаний.
Рис. 1.20. Структура экспертной системы, построенной на правилах.
Одна из проблем, с которой столкнулись разработчики экспертных систем, состояла в сложности пересмотра знаний после того, как они были закодированы в механизме правил. Накопление новых данных в экспертных системах позволяло увеличивать объем знаний, но при этом новые правила не позволяли отменить старые. Этого недостатка были лишены конкурирующие системы машинного обучения, которые в отличие от систем, построенных на правилах, могли быть переобучены на новых данных и не требовали непосредственного контакта с экспертом.
Одним из примеров применения методов символьного ИИ можно назвать семантический поиск, который развивают провайдеры поисковых сервисов. Семантический поиск пытается использовать намерения пользователя и семантику слов для поиска нужного контента. Он выходит за рамки подбора релевантных ссылок просто, по ключевым словам, используя информацию, которая может не присутствовать непосредственно в тексте (сами ключевые слова), но тесно связана с тем, что хочет найти пользователь. Например, найти куртку по запросу “куртка” достаточно тривиально, но если, например, человек формулирует вопрос в виде фразы “теплая одежда для зимы”, то вполне возможно, что ему подойдет сайт, где продается теплая куртка, при этом, может быть, пользователь ищет свитер или занят поиском термобелья. Для того чтобы выдать такой исчерпывающий ответ, нужно найти связь между всеми этими понятиями.
Данную идею наглядно иллюстрирует рис. 1.21.
Рис. 1.21. Схематическое изображение возможностей семантического поиска.
Семантический поиск – это подход, который обеспечивает более тесное смысловое соответствие между текстом поискового запроса и результатами поисковой выдачи на основе анализа намерений пользователя, осуществляющего поиск, контекста его запроса и взаимосвязи между словами.
Понимание взаимосвязи между словами, отношений между сущностями позволяет улучшить качество поиска. Для решения данной задачи используются уже упомянутые нами графы знаний. По данным компании Google, она начала первой использовать графы знаний для реализации семантического поиска в 2012 году. В это время в компании появился лозунг “сущности и контекст, вместо строк ключевых слов”, известный также в короткой его форме “сущности, а не строки”. Граф знаний объединяет большой объем общедоступной информации о различных сущностях и их признаках, свойствах и связях между этими сущностями. В 2013 году в поисковой системе Google появился алгоритм Hummingbird (Колибри), который считается первым поисковым алгоритмом, в котором был реализован семантический поиск, направленный на решение задачи “страницы, соответствующие смыслу, должны быть в приоритете по сравнению со страницами, соответствующими лишь нескольким поисковым словам”. По сути, это означает, что страницы, которые лучше соответствуют контексту и намерениям пользователя, должны ранжироваться выше, чем страницы, которые повторяют ключевые слова без контекста. Для поисковиков это было очень важно, учитывая, что появилось множество недобросовестных методов для поднятия рейтинга страниц путем накачки ключевых слов. В настоящее время графы знаний широко используются технологическими гигантами, которым необходим анализ огромных объемов неупорядоченных данных. Не только Google использует графы знаний. Facebook также использует данную форму организации информации, чтобы отслеживать сети людей и связи между ними, с учетом такой информации, как любимые фильмы и актеры, посещенные мероприятия и т. п.
Netflix так же, как и упомянутые поисковые системы, использует технологию графов знаний для организации информации о своем обширном каталоге контента, устанавливая связи между фильмами, телепередачами, актерами и режиссерами ( рис. 1.22), что помогает предсказывать будущие запросы клиентов.
Рис. 1.22. Граф знаний как основа семантического поиска.
Можно сказать, что семантический поиск – это технология, которая использует модель графа знаний и позволяет системам искусственного интеллекта понимать значение сущностей и связей между ними, давая таким образом возможность увеличить точность поиска и степень его персонализации.
Таким образом, графы знаний – это инструмент сбора информации из разнородных источников и структурирования большого количества взаимосвязанных данных, которые можно исследовать с помощью запросов. Графы знаний используются для создания таких систем, как семантические поисковые системы, рекомендательные системы и разговорные боты.
Несмотря на то, что по массовости применения в решении современных задач ИИ символьный ИИ уступил позиции субсимвольным методам, тем не менее применение символьного ИИ существует и по сей день в современных экспертных системах, таких как, например, платформа ROSS, которая помогает юридическим фирмам в изучении судебных дел, в поисковых системах и других приложениях.
Каждое из направлений ИИ имеет свои сильные и слабые стороны. Многогранность явления ИИ говорит о том, что не существует одного-единственного наилучшего способа для решения широкого спектра задач ИИ. Оптимальные решения могут быть достигнуты на базе комбинирования нескольких подходов. Например, разработки в области символьного ИИ лежат в истоках такого фундаментального направления в области ИИ как NLP (Natural Language Processing, обработка естественного языка), которое в последнее время активно развивается, опираясь на технологии глубокого обучения. Все чаще возникают проекты, в которых речь идет об интеграции символьных и субсимвольных подходов для обеспечения объяснимости ИИ-решений. Прежде чем привести примеры подобных решений, напомним читателю более подробно о сути коннекционистских подходов в создании ИИ.
Коннекционизм
Коннекционизм – от английского слова Connect (соединять) – это направление ИИ, которое исходит из предположения, что ментальные способности человека и, в частности, способность к обучению можно объяснить и имитировать на основе сложноорганизованной сети связанных между собой (соединенных определенным образом) одинаковых относительно простых элементов.
Одним из центральных направлений коннекционизма является моделирование интеллекта с помощью искусственных нейронных сетей, состоящих из нейронов и синапсов (связей между нейронами). Механизм работы искусственных нейронов заимствован из живой природы. Последние были созданы в результате наблюдения за процессами, происходящими в мозге живых организмов. Заметим, что сам термин “нейрон”, используемый в понятии “искусственные нейронные сети” (ИНС), был заимствован из биологии. Представление о том, что развитие и обучение человека базируется на свойствах нейронов мозга устанавливать связи, не ново, согласно данным данная идея была высказана еще в 1932 г. психологом из Колумбийского университета (Нью-Йорк) Эдвардом Торндайком.
Как известно из биологии, нервные клетки при определенном воздействии могут переходить в активированное состояние. Сигналы по нервным волокнам передаются в виде коротких импульсов от клетки к клетке, достигают нервных клеток в мышцах, что приводит к возбуждению мышечных волокон и, соответственно, к движению животного или человека.
Каждая нервная клетка состоит из трех частей: из тела, нескольких ветвистых отростков (дендритов) и протяженного нервного волокна (аксона), длина которого может составлять от нескольких миллиметров до десятков сантиметров (рис. 1.23).
Рис. 1.23. Упрощенная схема передачи сигнала в биологических нейронах
Нервные клетки взаимодействуют между собой в местах стыка (синапсах), где встречаются аксон пресинаптического нейрона и дендрит постсинаптического нейрона. Дендриты являются входными каналами для нервных импульсов, поступающих через аксоны от других нейронов. Эти импульсы могут либо возбуждать (увеличивать), либо подавлять (уменьшать) мембранный потенциал тела нейрона, который со временем возвращается к своему нормальному значению. Если количество возбуждающих импульсов превышает пороговое значение, то нейрон сам генерирует импульс.
Взаимодействующие между собой посредством передачи возбуждений нейроны формируют нейронные сети.
Как будет показано далее, ИНС используют некоторую аналогию с работой живых нервных клеток.
Основополагающей работой, заложившей фундамент для создания искусственных моделей нейронов и нейронных сетей, явилась работа Уоррена С. Мак-Каллока и Вальтера Питтса “Логическое исчисление идей, относящихся к нервной активности”, опубликованная в 1943 г., в которой была предложена модель формального нейрона. Однако прошло более 10 лет, прежде чем появился нейрон Розенблатта, в котором использовалось суммирование входящих сигналов, умноженных на соответствующие числовые значения (синаптические веса) – рис. 1.24.
Рис. 1.24. Схема формального нейрона Розенблатта
Несложно проследить сходство схемы, показанной на рис. 1.24, и рисунка 1.24. Модель, прообразом которой является биологический нейрон, представляет собой устройство, имеющее несколько входов (синапсы) и один выход (аксон).
На вход подаются сигналы . Каждому входу ставится в соответствие некоторый весовой коэффициент .
Попадая в нейрон, сигналы умножаются на соответствующие веса и складываются между собой ( – линейное преобразование). Сложение сигналов, поступающих по синаптическим связям, осуществляется в сумматоре (рис. 1.24).
Известно, что последовательное применение нескольких линейных преобразований эквивалентно одному линейному преобразованию. Если бы модель нейрона ограничивалась одним сумматором, то объединение множества нейронов в сеть было бы эквивалентно одному нейрону. Для того чтобы нарушить это правило, в модель нейрона добавляется нелинейный преобразователь (который реализует нелинейную функцию, которая называется функцией активации).
В рассмотренной модели использовалась пороговая функция активации (ступенчатая функция), которая показана на рис. 1.25 (а). Если суммарный сигнал превышает заданный порог активации, то нейрон возбуждается (активируется) и выдает на выходе 1, иначе выдается 0.
Определенным недостатком (ограниченной гибкостью) модели Уоррена Мак-Каллока являлся именно вид переходной функции (пороговый) – если значение вычисленного суммарного сигнала даже незначительно не достигает заданного порога, то выходной сигнал не формируется.
Такая функция подходит для бинарной классификации, но не подходит, когда для классификации требуется большее число нейронов (количество возможных классов больше двух). То есть если возникает задача, в которой возможно несколько ответов, или нам нужно вероятностное решение, например, с вероятностью 70% это один класс, а с вероятностью 30% – другой.
Впоследствии были реализованы модели нейрона с различными функциями активации. В частности, наиболее широкое использование получила сигмоида – гладкая монотонно возрастающая нелинейная функция, которая ограничена двумя горизонтальными асимптотами, что обеспечивает нормализацию выходного значения нейрона (рис. 1.25 б ) в диапазоне от 0 до 1.
По сути, нейрон представляет собой элементарный вычислитель, характеризующийся входным/ выходным состоянием и функцией активации.
Рис. 1.25. Ступенчатая функция (а) и сигмоидная (б)
На основе элементарных вычислителей, каждый из которых получает сигналы и посылает другим вычислителям, составляются ИНС разной топологии. Самая простая однослойная сеть показана на рис. 1.26.
Рис. 1.26. Однослойная нейронная сеть
Здесь сигналы от входного слоя сразу подаются на выходной слой по связям, каждой из которых устанавливается свой весовой коэффициент.
С помощью подобной сети можно построить работу простейших автоматов. Например, на рис. 1.27 показан автомат (гусеничный робот с тремя датчиками света), реагирующий на положение источника света.
Рис. 1.27. Упрощенная схема робота на гусеничном ходу, следующего за источником света.
Входные ячейки (фотоэлектрические датчики) реагируют на свет, посылают сигналы на выходные ячейки (нейроны), которые подают сигнал на управление гусеницами робота. Обучить такой автомат разным вариантам движения в зависимости от положения света можно задав весовые коэффициенты, определяющие силу связи между ячейками. В рассмотренном примере задача по обучению робота состояла в необходимости обеспечения движения такой машины за источником света. Для этого были подобраны веса, определяющие силу связи (от 0,45 до 0,99), как показано на рисунке. Еслиположение источника света находится спереди слева от автомата, то активируется вращение правой гусеницы, и наоборот. Несложно представить, что подобная машина будет двигаться за источником света.
Мы рассмотрели простейшую однослойную сеть. Больший интерес представляют многослойные сети. На рис. 1.28 показана многослойная сеть, где каждый нейрон одного слоя посылает сигнал каждому нейрону другого слоя. Данная сеть – это сеть прямого распространения, то есть сеть, в которой сигнал распространяется от входного слоя к выходному в одном направлении.
В показанной на рис. 1.28 сети пять слоев – один входной, три скрытых (промежуточных) и один выходной. Чем больше количество слоев, тем глубже сеть, поэтому и появился термин “глубокое обучение”. Формально при наличии больше одного скрытого слоя уже принято говорить о глубоких нейронных сетях, сети с одним скрытым слоем называют неглубокими (shallow).
Рис. 1.28. Многослойная сеть прямого распространения
Далее поговорим об обучении нейронных сетей. В процессе обучения на вход подается вектор признаков ( рис.1.28), описывающий объект (массив значений), число элементов которого равно числу входных нейронов, на внутренних слоях происходит обработка сигналов, сеть преобразовывает сигнал в выходной слой.
Для того чтобы более наглядно объяснить, как происходит процесс обучения, рассмотрим конкретную задачу распознавания рукописных символов (рис. 1.29).
Как показано на рисунке, изображение рукописного символа (в данном случае цифры 4) разбивается на пикселы, представляется в виде вектора чисел и подается на вход сети.
Если бы все символы были одного размера и начертания, то задача распознавания была бы предельно простой – в том смысле, что сети потребовался бы всего лишь один входной вектор, чтобы запомнить один правильный ответ. Но цифры могут быть напечатаны разными шрифтами, а если мы говорим про рукописные символы, то тут разнообразие еще больше. Все люди пишут числа по-разному – наклон, начертание (все то, что мы называем почерком). И если мы подадим сети, обученной на одном примере, немного измененный входной вектор, соответствующий несколько иному начертанию той же цифры, то правильного ответа уже не получим.
Если необходимо, чтобы сеть классифицировала все многочисленные варианты рукописного написания цифр (например, четверки, показанной на рисунке как числа “4”), то задача состоит в том, чтобы научить сеть способности обобщать признаки на различных входных данных.
Для этого сети нужно продемонстрировать максимально полный набор вариантов написания цифры разными способами, чтобы она “поняла”, какая совокупность признаков позволяет людям относить все разные начертания к одному классу изображений (цифре четыре). Для решения подобной задачи создаются обучающие выборки – данные, по которым обучается сеть. Обучение производится на многочисленных примерах размеченных данных, то есть на базе изображений, в каждом из которых отмечен правильный результат. Подобное обучение называют обучением с учителем или контролируемым обучением. Этот процесс похож на обучение ребенка. Ученику показывают изображение цифры в курсе или написав ее на доске, сообщая при этом правильный ответ. А потом тестируют ученика на знание предмета. Похожая процедура проводится с сетью. Сеть обучают на большом числе примеров по многочисленным вариантам написания каждой цифры, в результате чего подбираются весовые коэффициенты всех связей нейронов, и сеть в результате этой операции приобретает способность распознавать те изображения рукописных цифр, которые ей ранее не были продемонстрированы. После того, как сеть обучена, качество полученной модели проверяют на тестовой выборке. Если тест пройден – модель готова.
На рис. 1.29 условно мы показали процесс распознавания рукописной цифры 4. Затемненные кружки на рисунке отражают процесс возбуждения (активаций) нейронов, приводящих к получению ответа на выходном слое. Темным цветом показана искомая цифра, а светло-серым в выходном слое обозначены нейроны, соответствующие цифрам 1 и 7, что отражает тот факт, что написание этих цифр имеет некоторые схожие признаки с цифрой “4”.
Жизненный цикл нейронной сети, как и любой модели машинного обучения, состоит из двух этапов: обучение (training) и применение (inference). На рис. 1.30 показаны периоды обучения сети: 1 иллюстрирует сеть определенной топологии до начала обучения, 2 показывает процесс обучения. Речь идет о задаче, в которой сеть должна обучиться относить изображения к одному из двух классов – “кошка” и “собака”. По аналогии с предыдущим примером, где речь шла о необходимости продемонстрировать сети все варианты написания цифр, в данном случае сети необходимо продемонстрировать все варианты расположения, все ракурсы, все варианты освещения изображений обоих животных, чтобы сеть могла вычленить общие признаки для распознавания каждого из двух классов на фото. По мере того, как в сеть подаются размеченные изображения (про каждое известно, что там показано – кошка или собака), идет процесс обучения, который состоит в том, чтобы так подобрать весовые коэффициенты, чтобы сеть правильно относила каждое изображение к одному из двух классов. На рисунке на стадии обучения нейроны показаны разных размеров, что условно означает процесс нахождения весовых коэффициентов, которые определяют разную силу связи между соседними нейронами (то есть вес отдельных нейронов). На рис. 1.30 (3-4) условно показан процесс оптимизации сети по производительности: производится удаление избыточных связей в сети – связей, которые определяются малыми весами.
Рис. 1.30. Стадии обучения искусственной нейронной сети. Источник: адаптировано по материалам
На рис. 1.31 представлена более подробная схема, иллюстрирующая стадии обучения и применения нейронной сети с привязкой к ИТ-инфраструктуре. В верхней части диаграммы показана система приема и обработки данных. Левая ветвь показывает процесс обучеия модели.
В случае глубокой нейросети на вход подаются тысячи и более размеченных данных, на которых сеть должна обучиться, чтобы идентифицировать закономерности в данных. Обучение обычно требует больших затрат вычислительных ресурсов, процесс обучения может быть реализован на локальном оборудовании или в облаке.
Обученная и оптимизированная модель передается в систему, где происходит ее применение – сеть распознает новые изображения. Заметим, что обучение сети может являться довольно длительным процессом, а вычисление результатов обученной сетью модели происходит достаточно быстро. Готовая для использования модель может быть размещена в облаке в некотором ЦОДе, локально у заказчика или на периферийном устройстве. В случае периферийного устройства небольшой мощности может быть особенно актуальна стадия оптимизации модели по производительности, о которой мы упомянули ранее.
Рис. 1.31. Основные элементы системы обучения и применения искусственной нейронной сети. Источник: адаптировано по материалам Gartner
Выше мы отметили, что для обучения модели на базе нейронных сетей необходимо настроить оптимальные веса для всех связей. Но до сих пор не обсуждали, как это можно сделать.
В сети из нескольких нейронов, как в примере рис. 1.27, весовые коэффициенты можно подобрать вручную. Однако в большей сети необходим автоматический способ поиска оптимальных значений весов (алгоритм обучения). Во время обучения веса, изменяясь на малые величины, приближаются к целевым (оптимальным) значениям.
Важнейшим этапом в развитии нейросетевых подходов явилось появление в середине 80-х годов прошлого века алгоритма обучения, который называется “метод обратного распространения ошибки”. Не вдаваясь в детали, кратко остановимся на сути этого алгоритма.
Обучение нейросети происходит в два этапа – прямого распространения сигнала по сети, после которого вычисляется ошибка предсказания, и распространения ошибки по сети в обратную сторону по тем же самым связям, при котором веса связей сети корректируются таким образом, чтобы повысить успешность решения сетью задачи (уменьшить ошибку). Процесс повторяется до тех пор, пока не будет достигнут желаемый результат.
Поясним процедуру на рассмотренном выше примере с классификацией изображений. На стадии обучения мы представляем нейронной сети изображения вместе с метками (целевыми значениями), которые определяют, что именно изображено на рисунке. Предположим, что на некотором шаге обучения мы предоставили сети изображение кошки. После завершения прямого прохождения данных об изображениичерезсетьмодельформируетвыход, согласно которому изображение на 75% является кошкой. Во время обратного распространения учитывается ошибка, полученная на предыдущем этапе. Веса сети корректируются с учетом ошибки, так, чтобы в следующий раз точность была выше. Корректировка каждого веса осуществляется пропорционально его индивидуальному вкладу в общую ошибку. Поскольку вклад в ошибку от весов в более ранних слоях зависит от вклада весов в более поздних слоях, сигнал ошибки описывается как “обратное распространение ошибки”.
Задача может быть сформулирована как оптимизация некоторой функции потерь, которая зависит от искомых весов. Потери (ошибка) – это разница между текущим предсказанием сети и истинным (определяемым меткой). Веса изменяются на каждой итерации, пока мы не приблизимся к минимуму функции потерь. Цель обучения – минимизировать ошибку или максимизировать точность предсказания, выполняемого моделью.
Символизм и коннекционизм – конкуренция и интеграция
Как мы отметили, символизм и коннекционизм не единственные подходы, на основе которых могут строиться системы искусственного интеллекта. Но прежде, чем упомянуть другие системы, интересно остановиться на сравнении символьного и коннекционистского подходов, поскольку они представляют собой две основные ветви искусственного интеллекта и процесс их развития, конкуренции и взаимо-дополнения в известной степени отражает процесс эволюции ИИ.
Сравнивая упомянутые направления, уместно напомнить понятия “нисходящий” и “восходящий” как два подхода к созданию ИИ. Символьный подход относят к нисходящему (его также иногда называют подход “сверху вниз”), а коннекционистский – к восходящему (или к подходу “снизу вверх”).
В нисходящем подходе познание рассматривается как высокоуровневое явление, которое не зависит от низкоуровневых деталей, то есть абстрагируется от способа реализации механизма работы мозга (в случае природного интеллекта) или принципа действия, конструкции вычислительного устройства (в случае искусственного интеллекта).
Подход “снизу вверх”, или так называемая “восходящая парадигма” – это процесс изучения механизмов, использованных природой, с тем чтобы на их основе создать тот или иной вариант реализации ИИ. Примером последнего подхода является процесс создания искусственных нейронных сетей, которые базировались на изучении нейросетевой структуры мозга животных и человека.
Использование вышеописанных подходов можно проиллюстрировать на разных вариантах построения программы распознавания символов – например, символы можно распознавать на основе описания начертания той или иной буквы, в виде определения совокупности правил: “если буква состоит из трех отрезков, двух длинных и одного короткого, которые расположены таким-то образом, то следовательно – это буква А”. Это символьный или нисходящий подход. В восходящем подходе речь может идти об обучении нейронной сети путем представления ей изображений большой совокупности букв “А”, написанных разными способами, так что сеть сможет вычленить общие признаки для всех вариантов написания буквы и начать ее распознавать.
Исторически символьный подход был первым направлением, на базе которого удалось создать коммерчески успешные системы искусственного интеллекта. Он господствовал примерно с 1950-х по 1980-е годы.
Нисходящие системы плохо справляются с решением задач, включающих большое количество слабых видов взаимодействий, как, например, в системах распознавания образов. Этим объясняется растущее стремление найти альтернативный, более гибкий подход – что стимулировало обращение к коннекционистским моделям.
Для обучения ИНС требуют больших вычислительных ресурсов и памяти, которые было невозможно удовлетворить в период расцвета символьных методов. Позднее, когда появились более производительные компьютеры, исследования коннекционистских сетей “подход снизу вверх” показали значительные перспективы сначала в области распознавания образов, а позднее и во многих других областях. Общая тенденция выразилась в том, что по мере роста вычислительных возможностей коннекционистские методы в существенной мере потеснили символьные.
Этот процесс наглядно иллюстрирует рис. 1.32, на котором показано соотношение числа цитируемых публикаций, принадлежащих к категориям “Коннекционизм” и “Символизм”. Корпус статей “Коннекционизм” включал более 100 тысяч публикаций, собранных на “Web of Science”, а корпус “Символизм” – примерно 65 тысяч публикаций, собранных по профильным ключевым словам.
Рис. 1.32. Соотношение числа цитируемых публикаций “Коннекционизм”/ “Символизм” (логарифмическая шкала). Источник: адаптировано по материалам. Примечание: ONR – Ofice of Naval Research (Управление военно-морских исследований США)
На рис. 1.32 отмечен 1943 год, в котором, как мы упомянули, появилась модель МакКаллока-Питтса.
Согласно данным Британики, первая нейронная сеть появилась в 1954 году, она была разработана Белмонтом Фарли и Уэсли Кларком из Массачусетского технологического института. Сеть была ограничена 128 нейронами и позволяла распознавать простые шаблоны.
Два года спустя (в 1960 году) в Корнеллском университете был продемонстрирован первый нейрокомпьютер – “Марк-1”, который был способен распознавать некоторые буквы английского алфавита. В современной терминологии перцептроны могут быть классифицированы как искусственные нейронные сети с одним скрытым слоем, с пороговой передаточной функцией и с прямым распространением сигнала.
В это же время шло развитие технологий в области символьного ИИ. В частности, на рис. 1.32 отмечен 1965 год – это год, в котором британский философ и логик Джон Алан Робинсон сформулировал правило резолюций – правило вывода, восходящее к методу доказательства теорем через поиск противоречий. Работы ученого были решающими в развитии языка логического программирования Пролог, оказавшего большое влияние на развитие символьного направления.
Следующее событие, отмеченное на временной шкале рис. 1.32, это 1969 год – год, когда Марвин Минский и Сеймур Пейперт написали книгу под названием “Перцептроны”, в которой были отмечены некоторые ограничения перцептронов, публикация способствовала смещению интереса исследователей искусственного интеллекта в область символьных вычислений.
С середины 70-х годов прошлого столетия до начала восьмидесятых наблюдался, как мы уже упомянули, период охлаждения к теме ИИ. Выход из данной зимы искусственного интеллекта произошел на волне развития экспертных систем.
Однако в конце 1980-х и начале 1990-х годов индустрия ИИ испытала ряд финансовых неудач. На рис. 1.32 этот период обозначен как крах рынка LISP машин. В конце 80-х годов рынок специализированных аппаратных средств искусственного интеллекта испытал давление со стороны настольных компьютеров Apple и IBM, которые быстро набирали вычислительную мощность и вскоре сделали неэффективными более дорогие LISP-машины, что привело к закрытию целой индустрии.
1986 г. отмечен как год появления алгоритма обратного распространения ошибки – популярного алгоритма обучения нейронных сетей, в существенной мере способствовавшего распространению нейросетевых технологий. Алгоритм часто связывают с именем Румельхарта, который внес существенный вклад в развитие метода.
С середины 90-х годов нейронные сети привлекают все больший интерес сообщества разработчиков ИИ.
Глубокие нейронные сети позволили получить ранее недостижимые результаты в задачах предсказания, однако они не дают объяснения человеку того, как именно был достигнут тот или иной результат (не являются интерпретируемыми), что ограничивает их применение особенно в таких приложениях, в которых принятие решения является критичным с точки зрения последствий при неверно принятом решении (например, постановка диагноза и выбор метода лечения).
Если логика семантической сети изначально понятна человеку, то с нейронными сетями такую логику проследить невозможно, что демонстрирует рис. 1.33.
Рис. 1.33. Сравнение символьного и коннекционистского подходов. Источник: Марвин Минский 1991 г.
Наличие недостатков и достоинств в нейросетевом и символьном подходах стимулировало исследователей к созданию гибридных решений. Гибридный подход, известный как нейросимвольный ИИ, сочетает в себе черты двух основных стратегий ИИ символьного и коннекционистского (рис. 1.34).
Рис. 1.34. Гибридный нейросимвольный ИИ.
В символьном ИИ (вверху слева) человек-эксперт должен предоставить “базу знаний”, которую ИИ использует для ответа на вопросы. Глубокие сети (вверху справа) обучаются для получения правильных ответов. Гибридное решение использует глубокие сети для того, чтобы генерировать части базы знаний, необходимые для ответа на заданный вопрос, или формируют признаки, использующиеся далее в процессе вывода.
Мы уже говорили, что там, где критичность принятия решения высока, необходимо решение, где человек контролирует ИИ. Те же соображения справедливы в отношении объяснимости ИИ там, где решение критично с точки зрения недопустимости ошибки, там требуется объяснение – как, на основании чего ИИ принял решение.
Объяснимый искусственный интеллект, или XAI (сокращение от Explainable Artificial Intelligence), – одно из относительно молодых и быстро развивающихся направлений в области ИИ, о котором речь еще будет идти в данном курсе.
Эволюционизм
Эволюционизм можно определить как научное направление, в рамках которого разрабатывается совокупность алгоритмов, моделирующих эволюционные процессы (и механизмы их реализации), наблюдаемые в живой природе. Эти механизмы обеспечили возникновение сложнейших живых организмов на Земле, приспособленных к самым разным условиям обитания. Исследование и использование данных механизмов позволило человеку создать искусственные системы, проявляющие способности достижения оптимальных стратегий поведения в разных внешних условиях. Подобно тому как искусственные нейронные сети получили начало на основе изучения работы нейронов в живых организмах, так эволюционные алгоритмы базируются на наблюдаемых в живой природе процессах наследования, мутации и отбора.
Отметим, что идея построения эволюционных алгоритмов ненамного моложе идеи построения искусственных нейронных сетей. Первые попытки использования цифровых компьютерных моделей для изучения процессов естественной эволюции использовались уже с середины 1950-х годов.
В начале 60-х годов прошлого столетия Ганс-Иоахим Бремерманн представил одни из первых попыток применить моделируемую эволюцию для решения задач численной оптимизации, а также разработал некоторые из ранних теорий эволюционных алгоритмов.
В 1967 году Джоном Генри Холландом были разработаны наиболее значимые генетические алгоритмы (подмножество эволюционных алгоритмов), на базовых принципах работы которых мы коротко остановимся.
Генетический алгоритм – это эвристический поисковый алгоритм, который базируется на идеях теории эволюции Дарвина, которая в самом общем плане утверждает, что эволюция обусловлена небольшими вариациями признаков особей, которые усиливаются под воздействием естественного отбора. Особи с полезными признаками имеют больше шансов размножиться и передать эти признаки потомству, чем организмы с вредными признаками.
Генетический алгоритм моделирует процесс естественного отбора, в котором наиболее приспособленные особи отбираются для производства потомства следующего поколения. Эти наиболее приспособленные особи из популяции производят потомство, которое наследует характеристики родителей, и эти характеристики передаются следующему поколению. Данный процесс продолжается при смене поколений (итерационно) и в конце концов приводит к “искомому” поколению с наиболее приспособленными особями. По сути, этот процесс можно рассматривать как итерационный процесс нахождения наилучшего решения задачи.
В самом общем плане итерационный процесс выглядит следующим образом: экспертом выбирается упрощенное прикидочное решение и проверяется, насколько оно удачно. Если оно удовлетворяет условиям, предъявляемым к решению, то задача выполнена, если решение не удовлетворяет требованиям, то оно модифицируется случайным образом и опять проверяется, не удовлетворяет ли требованиям модифицированное решение. При этом если в реальной жизни смена поколений растений и животных – это длительный селективный процесс, то используя генетический алгоритм можно сократить время между поколениями до считанных секунд компьютерных вычислений.
Можно сказать, что генетический алгоритм позволяет заменить процесс моделирования объекта, отвечающего некоторым требованиям, на процесс моделирования эволюции, приводящий к появлению подобного объекта.
Рассмотрим принципы работы генетического алгоритма на упрощенном наглядном примере.
Задача формулируется так, что ее решение может быть представлено в виде вектора генов (генотипа), где каждый ген может быть представлен некоторым объектом (числом или битом). На рис. 1.35 показана схема, поясняющая соотношение понятий ген, хромосома, популяция, используемых в генетическом алгоритме. Подобно тому как в алгоритмах на базе искусственных нейросетей базовый термин “нейрон” заимствован из нейробиологии, в генетических алгоритмах применяется целый ряд терминов, изначально введенных в генетике (популяция, особь, ген, хромосома, генотип).
В проекте было показано, что случайное разрушение до 10% нейронов в обученной сети не влияло на производительность сети – что напоминает свойство мозга человека переносить ограниченный ущерб, нанесенный хирургическим вмешательством или болезнью.
Среди первых применений можно упомянуть использование сети для принятия инвестиционных решений, распознавания рукописных цифр и определение по внешнему виду некоторых видов вооружений на изображениях.
В 1958 году Розенблатт построил электронное устройство, которое должно было имитировать процессы человеческого восприятия, получившее название “Перцептрон”. Проект базировался на развитии идей МакКаллока и Питтса. Перцептрон должен был передавать сигналы от устройства на базе фотоэлементов в блоки электромеханических ячеек памяти, которые оценивали относительную величину электрических сигналов.
Особь (индивидуум) характеризуется набором параметров – фенотипом. Фенотип – это совокупность внешних и внутренних признаков организма, приобретенных в результате индивидуального развития. Фенотип формируется на основе генотипа (совокупность генов) при участии ряда факторов внешней среды.
Гены соединяются в строку, образуя хромосому (решение). Совокупность хромосом дает популяцию, где любая хромосома есть возможное решение рассматриваемой оптимизационной задачи.
Процесс поиска решения осуществляется в рамках алгоритма, показанного на рис. 1.36.
Рис. 1.36. Блок-схема генетического алгоритма.
На первом этапе осуществляется создание популяции. На этом этапе (как правило, случайным образом) создается множество генотипов начальной популяции. В терминах генетического алгоритма популяция – это множество возможных решений имеющейся задачи (хромосом), которые образуют пространство поиска.
На втором этапе идет оценивание приспособленности особей (хромосом) в популяции. На этом этапе осуществляется вычисление так называемой функции пригодности или фитнес-функции. Фитнес-функция определяет пригодность, приспособленность особи (описываемой хромосомой), то есть ее способность конкурировать с другими особями. Вероятность того, что особь будет выбрана для размножения, зависит от оценки ее приспособленности.
Фитнес-функция принимает на входе текущее потенциальное решение задачи и выдает значение, оценивающее его пригодность.
На следующем шаге идет проверка выполнения условия остановки алгоритма. Алгоритм прекратит исполняться, если найдено решение, удовлетворяющее требуемому критерию качества, если полученное значение больше не улучшается, если исчерпано число отпущенных на задачу поколений или лимит времени на эволюцию.
Если условие остановки не выполнено, то производится отбор хромосом для производства потомков. Идея фазы отбора заключается в том, чтобы отобрать наиболее приспособленных особей (хромосом) и позволить им передать свои гены следующему поколению.
Особи с высокой приспособленностью имеют больше шансов быть отобранными для воспроизводства. Процесс скрещивания показан на рис. 1.37(а). Для каждой пары родителей, подлежащих размножению случайным образом, выбирается точка кроссинговера (точка разрыва). В этой точке обе хромосомы делятся на две части и обмениваются генетическим материалом. На рис. 1.37(а) точка кроссинговера равна 3. Потомство создается путем обмена генами родителей между собой до достижения точки кроссинговера. Новое потомство добавляется в популяцию.
Некоторые из генов образовавшихся потомков могут подвергнуться мутации для поддержания разнообразия в популяции. На рис. 1.37(б) данный процесс проиллюстрирован тем, что некоторые нули заменены на единицы, а единицы на нули. Есть определенная вероятность, что благодаря мутации особь приобретет новое полезное свойство, если это свойство будет вредным, то такая особь будет отсеяна.
Рис. 1.37. Упрощенная схема, поясняющая работу процессов скрещивания и мутации.
Таким образом, для возникновения новых комбинаций генов используются две операции: кроссинговер (скрещивание), позволяющий создать две новые хромосомы потомков путем комбинирования генетического материала пары родителей, а также мутация, которая может вызывать изменения в отдельных хромосомах.
Со временем эволюционные методы стали применять для оптимизации структуры нейросети, так возник термин “нейроэволюция”. Первые нейроэволюционные алгоритмы появились в 1980-х годах.
В самом общем плане концепция нейроэволюции исходит из того, что по мере эволюции человеческий мозг развивался и эволюционировал, обретая способность все лучше решать определенные задачи. Идея нейроэволюции – запустить эволюционный процесс, подобный тому, который привел к развитию нашего мозга, на базе изменения искусственных нейронных сетей с использованием эволюционных алгоритмов.
Нейроэволюция – это метод машинного обучения, который применяет эволюционные алгоритмы для построения искусственных нейронных сетей. Общей целью является такая эволюция искусственных нейронных сетей, которая приводит к решению определенных задач.
Обучение нейросетей с помощью нейроэволюции наиболее эффективно в задачах обучения с подкреплением, таких как поиск оптимальных стратегий в компьютерных играх. В отличие от классических задач машинного обучения, в них удачность стратегии определяется не на каждом этапе игры, а в конце.
Нейроэволюция позволяет найти нейронную сеть, которая оптимизирует свою работу, учитывая вышеописанную обратную связь, без прямой информации о том, что именно она должна делать.
Существуют нейроэволюционные алгоритмы, которые эволюционно изменяют веса связей при заданной топологии сети, а есть алгоритмы, которые помимо эволюции весов также производят эволюцию топологии сети. В качестве примера можно привести эволюцию поведения в компьютерных играх или управление мобильными роботами.
Принципиальная схема нейроэволюции показана на рис. 1.38.
Рис. 1.38. Принципиальная схема нейроэволюции.
На каждой итерации закодированная информация о нейросети в виде генов декодируется в соответствующую нейросеть, которая тестируется на решении целевой задачи. В качестве целевой задачи на рисунке показана некоторая внешняя среда, в которой необходимо выполнять определенные функции для того, чтобы достигать поставленной задачи. Например, речь может идти об участии в игре и, соответственно, необходимости выполнять действия, которые ведут к выигрышу. В процессе тестирования измеряется производительность исследуемой конфигурации нейросети в решении задачи (фитнес-функция). После оценки всех членов текущей популяции, с помощью рассмотренных выше генетических операторов создается новая популяция. Особи с большей фитнес-функцией заменяют особи с меньшей.
Приложения на базе нейроэволюции нашли применение во многих областях, включая обработку изображений, обработку речи, программную инженерию, построение систем кибербезопасности и используются в целом ряде отраслей, таких как здравоохранение, финансы, робототехника и т. п.
Агентный подход
Центральным элементом данного подхода к построению искусственного интеллекта, как следует из его названия, является понятие агента. Согласно, “агент – это любая сущность физическая или виртуальная, которая воспринимает свое окружение через датчики и действует на это окружение через исполнительные механизмы”.
Под агентом могут подразумеваться разные сущности (программа, робот, человек). Агенты могут действовать в реальном мире (роботы), в виртуальном (персонаж игры), воздействовать на внешний мир из виртуального – чат-боты и другие программные агенты, поддерживающие решения конкретных людей.
Тенденции в разработке программного обеспечения последних лет показывают устойчивое движение в сторону поддержки автономных, рациональных агентов. Для создания интеллектуальных агентов могут использоваться методы машинного обучения, символьный, эволюционный, нейросетевой и гибридные подходы.
Алгоритмы машинного обучения позволяют агенту адекватно реагировать на изменения среды, совершенствовать правила поведения или приобретать интеллектуальное поведение.
Агенты можно классифицировать по степени их интеллектуальности, по способности рассуждать. Самые простые агенты – это реактивные агенты, они имеют простейший тип поведения, основываются на минимальном объеме информации и простых правилах: “ситуация-действие”, “запрос-ответ”.
Так называемые делиберативные агенты используют некоторые логические рассуждения и/или возможности планирования (1.39).
Рис. 1.39. Реактивные (слева) и делиберативные (справа) агенты.
Агенты можно классифицировать по месту, где они выполняют свой код: статические агенты работают на выделенном сетевом узле, мобильные агенты могут перемещать свой код c одного компьютера на другой между узлами сети.
По поведению агенты можно разделить на пассивные (не имеют конкретных целей, могут реагировать на внешние раздражители, но сами не будут инициировать никаких действий) и активные (имеют определенные цели, которые они преследуют). Используется также термин “когнитивные агенты” – агенты, которые предполагают сложное планирование и рассуждения.
Агенты часто работают не поодиночке, а в рамках некоторой многоагентной системы. Многоагентная система – это слабо связанная сеть агентов, решающих некоторые задачи. Агенты работают вместе, чтобы найти ответы на вопросы, которые выходят за рамки индивидуальных возможностей или знаний каждого агента.
Многоагентные системы можно классифицировать по типу сотрудничества агентов (рис. 1.40).
Рис. 1.40. Классификация многоагентных систем по вариантам сотрудничества агентов.
Многоагентная система может иметь независимых агентов – каждый агент преследует свои собственные цели. В такой системе агенты могут не сотрудничать, но также возможен вариант, когда сотрудничество не запланировано, но может возникать спонтанно – в этом случае такие системы называют системами с эмерджентным сотрудничеством.
Многоагентные системы называются сотрудничающими, если у ее агентов есть общие цели, при этом ее агенты могут взаимодействовать между собой, а могут не взаимодействовать.
Сотрудничество внутри многоагентной системы может быть явно спроектировано разработчиком и может реализоваться путем адаптации, когда сотрудничество отдельных агентов развивается в ходе какого-то эволюционного процесса.
Многоагентный подход обеспечивает устойчивость и масштабируемость системы. За счет того, что ответственность за выполнение общей задачи распределена между большим числом агентов, система может переносить сбои одного или нескольких агентов.
Такие характеристики многоагентных систем, как гибкость и надежность, делают их эффективным подходом для решения многих сложных задач. Подобная задача делится на множество мелких простых подзадач, которые распределяются между агентами. Потребление ресурсов в такой системе оптимизируется между несколькими агентами, что часто приводит к менее затратному решению по сравнению с подходом, при котором вся задача выполняется одним агентом.
Возможны разные типы многоагентных систем по способу организации агентов. В качестве примера на рис. 1.41 показана иерархическая и коалиционная организация. В первом случае отдельные агенты организованы в древовидную структуру, часто используемую при управлении сотрудниками в компании. Агенты, находящиеся выше по дереву, имеют более высокий уровень осведомленности. Данные, получаемые агентами нижнего уровня, передаются вверх, а управленческие распоряжения вниз. В коалиционном типе организации агенты группируются в соответствии со своими целями в группы агентов, имеющих схожие цели.
Рис. 1.41. Типы многоагентных систем по способу организации агентов
Подходы с использованием интеллектуальных агентов и много-агентных систем применяются во многих приложениях в разных отраслях – в компьютерных играх для придания интеллекта неигровым персонажам, в сетевых и мобильных технологиях для достижения автоматического динамического распределения нагрузки. Они также используются для обеспечения масштабируемости и самовосстановления сетей, для создания скоординированных оборонных систем, для приложений транспортной отрасли, в задачах логистики, в промышленном производстве, в энергетике, в эпидемиологии, в моделировании социальных систем и т. п.
Из конкретных примеров можно привести проект компании Waymo, которая создала среду многоагентного моделирования Carcraft для тестирования алгоритмов беспилотных автомобилей, где имитируется дорожное взаимодействие между водителями-людьми, пешеходами и самоуправляемыми автомобилями.
Символьный ИИ обозначает совокупность методов, в которых знания представляются в виде символов и их отношений, то есть в виде некоторого формального языка. Символьный ИИ основан на способности человека понимать мир путем формирования символьных представлений и их взаимосвязей и создавать правила для фиксации знаний. Способность общаться с помощью символов – одно из проявлений нашего интеллекта. Символы играют ключевую роль в процессе мышления и рассуждения человека.
С помощью символов мы можем представлять окружающие нас предметы (машина, кошка, собака). Это могут быть не только перечисленные материальные объекты, но и абстрактные понятия (демократия, капитализм, транзакция). Символы могут быть организованы в иерархию (автомобиль состоит из дверей, окон, шин, сидений и т. д.). Символы могут использоваться для описания других символов (красное яблоко, тяжелый груз). Способность человека манипулировать символами существовала тысячи лет до появления термина “искусственный интеллект”.
С помощью символов могут быть построены логические конструкции (если Петя является сыном моей дочери, то, следовательно, Петя мой внук). Символьный искусственный интеллект также иногда именуют как “Rule based AI” – ИИ, основанный на правилах. В некоторых публикациях в качестве синонима понятия “символьный ИИ” используют сокращение GOFAI (“Good Old-Fashioned Artificial Intelligence” – “старый добрый искусственный интеллект”), по имени, которое использовал Джон Хоугеланд в своего курса “Искусственный интеллект: Основная идея”.
Для обозначения альтернативных подходов, не использующих явно символы высокого уровня, используют термин “субсимвольный ИИ”.
Приведем простой пример применения подходов символьного ИИ на практике: пусть некая скоринговая программа использует символьные переменные “пол”, “возраст”, “профессия” и т. п., которые могут принимать определенные значения. В программе заданы правила типа “Если профессия “программист”, пол мужской, а возраст попадает в промежуток от 30 до 40 лет, то некоторая переменная, участвующая в определении кредитного рейтинга, примет такое-то значение”. При этом очевидно, что логика, по которой оценивается кредитный рейтинг респондента в данном примере задана изначально, вычисляется она по определенным правилам, может быть явно прочитана человеком, а подобного рода вывод программы является объяснимым. Определив совокупность правил вышеуказанным способом и задавая на входе совокупность параметров, по которым мы оцениваем потенциальных клиентов, можно решать такие задачи, как оценка целесообразности выдачи кредита.
Говорят, что символьный ИИ относится к объяснимым (или интерпретируемым) методам ИИ, поскольку позволяет рассуждать о том, каким образом получен достигнутый результат.
В рамках символьного подхода мы можем определить некоторую сущность набором признаков и связей. Например, яблоко-это фрукт, который растет на дереве, яблоко может быть красного, желтого или зеленого цвета и так далее (рис. 1.17).
Определив набор сущностей, выраженных в виде символов и отношений между ними, мы приходим к понятию ” семантические сети” – сети, которые представляют собой направленный граф, вершины которого соответствуют объектам, а дуги (линии) – отношениям между ними.
Достоинство семантических сетей состоит в том, что это человеко-читаемый наглядный способ представления знаний.
Примером семантической сети является граф, отражающий взаимодействия в семейной системе, где на основе указанных связей можно получить характер родственных отношений между всеми членами группы (рис. 1.18).
Используя в качестве семантической сети (базы знаний) семейное дерево, то есть зная имена и родственные связи и следуя цепочке рассуждений типа “Если Анна мать Елены, а Елена мать Евгения, то Евгений – это внук Анны”, система может генерировать ответы на вопросы о родственных отношениях всех участников системы.
Используя базу знаний, представляющую собой набор фактов, правил и отношений, символьная ИИ-система позволяет вести рассуждения, основанные на алгебраическом манипулировании имеющимися знаниями и отвечать на вопросы. Понятный человеку процесс получения выводов в символьных моделях облегчает контроль в их построении и отладке.
При этом отметим, что символьная система ИИ, по крайней мере в классическом ее понимании, не может обучаться сама, она опирается на базы знаний, которые явно закладываются в систему разработчиком.
Эффективность такой системы зависит от объема и качества базы знаний. Если система получает запрос, по которому знания либо отсутствуют, либо ошибочны, система не сможет дать удовлетворительный ответ.
Приведенный пример на рис. 1.18 ограничен набором людей, связанных заранее известными (родственными) отношениями, однако если попытаться построить граф взаимоотношений из случайного набора людей, задача окажется намного сложнее.
С точки зрения области применения, следует отметить, что символьный подход лучше всего работает в задачах с четко определенными правилами. Например, символьный подход показал хорошие результаты в доказательстве теорем, в программах для игры в шахматы.
В частности, символьный подход (наряду с другими методами) был использован в решении Deep Blue, победившем чемпиона по шахматам Каспарова в 1997 году.
Символьные подходы были доминирующей парадигмой исследований в области ИИ с середины 1950-х до середины 1990-х, они показали свою эффективность в задачах с четко заданными правилами, однако открытые системы, такие как задачи на ориентацию в “обыденной реальности мира”, слишком беспорядочны, чтобы представлять их в виде универсально обоснованных правил логики, которыми оперирует символьный ИИ.
Символьный подход в основном ориентирован на извлечение знаний из экспертов, однако существуют методы, извлекающие знания из данных. Примером такого подхода является алгоритм дерева решений – метод обучения с учителем. Цель алгоритма – создать дерево правил, которые можно использовать для прогнозирования выходных данных при заданных входных данных. Дерево решений – это тип направленного ациклического графа, который отображает решения и их последствия. Логика дерева решений наглядно представляется графом и понятна человеку. Деревья решений могут работать как с дискретными, так и с непрерывными переменными, их можно использовать для задач регрессии и классификации, речь о которых пойдет далее в этой лекции.
Дерево решений обычно начинается с одного узла, который разветвляется на возможные результаты. Каждый из этих результатов приводит к дополнительным узлам, которые разветвляются на другие возможности, что и позволяет говорить о древовидной структуре.
Пример дерева решений показан на рис. 1.19. Начиная с отправной точки “могу ли я начать писать статью”, решения принимаются в зависимости от последовательности ответов на вопросы, каждый из которых зависит от результатов предыдущих ответов. Так двигаясь по той или иной ветке дерева, мы достигаем результата.
Дерево решений – это простейший способ извлечения знаний из данных, существуют и другие. Такой подход изучается в рамках направления интеллектуального анализа данных (Data Mining) или “добычи знаний из баз данных” (Knowledge Discovery in Databases).
В первую очередь символьный ИИ ассоциируется с экспертными системами и базами знаний.
Экспертные системы были одними из первых действительно успешных форм программного обеспечения для ИИ. Экспертная система эмулирует способность человека-эксперта по принятию решений путем рассуждений на основе совокупности знаний, представленных в виде правил. Первые экспертные системы были созданы в 1970-х годах. К наиболее ранним примерам можно отнести программу MYCIN, которая была разработана в 1972 году и диагностировала инфекционные заболевания крови.
Другой пример – система PROSPECTOR, созданная в 1974-83 гг. для геологических изысканий.
Так же, как и MYCIN, PROSPECTOR вовлекает геолога в диалог, с тем чтобы, опираясь на его наблюдения в качестве источника исходных данных, выбрать модель и дать ответ на вопросы “Где бурить?” и “Где искать?”. В 1984 г. система достаточно точно предсказала существование месторождения молибдена, оцененного в многомиллионную сумму.
Широкое распространение экспертные системы получили в 1980-х годах. В 1980 году для корпорации Digital Equipment Сorp. была создана экспертная система под названием XCON, которая, по свидетельству разработчиков, экономила до 40 млн долларов ежегодно. С начала 1980-х годов корпорации по всему миру начали разрабатывать экспертные системы. Можно сказать, что выход из очередной зимы искусственного интеллекта в 1980-х годах произошел именно на волне разработок ИИ в форме экспертных систем. Основные элементы экспертной системы показаны на рис. 1.20.
Как видно из рисунка, одним из ключевых элементов системы является инженер по знаниям, который должен выудить из эксперта (и формализовать) тот набор знаний, которым этот специалист владеет. Иногда это является нетривиальной задачей, что связано не только с нежеланием некоторых экспертов делиться всеми знаниями, но и со сложностью вербализации и формализации некоторых знаний.
Рис. 1.20. Структура экспертной системы, построенной на правилах.
Одна из проблем, с которой столкнулись разработчики экспертных систем, состояла в сложности пересмотра знаний после того, как они были закодированы в механизме правил. Накопление новых данных в экспертных системах позволяло увеличивать объем знаний, но при этом новые правила не позволяли отменить старые. Этого недостатка были лишены конкурирующие системы машинного обучения, которые в отличие от систем, построенных на правилах, могли быть переобучены на новых данных и не требовали непосредственного контакта с экспертом.
Одним из примеров применения методов символьного ИИ можно назвать семантический поиск, который развивают провайдеры поисковых сервисов. Семантический поиск пытается использовать намерения пользователя и семантику слов для поиска нужного контента. Он выходит за рамки подбора релевантных ссылок просто, по ключевым словам, используя информацию, которая может не присутствовать непосредственно в тексте (сами ключевые слова), но тесно связана с тем, что хочет найти пользователь. Например, найти куртку по запросу “куртка” достаточно тривиально, но если, например, человек формулирует вопрос в виде фразы “теплая одежда для зимы”, то вполне возможно, что ему подойдет сайт, где продается теплая куртка, при этом, может быть, пользователь ищет свитер или занят поиском термобелья. Для того чтобы выдать такой исчерпывающий ответ, нужно найти связь между всеми этими понятиями.
Данную идею наглядно иллюстрирует рис. 1.21.
Рис. 1.21. Схематическое изображение возможностей семантического поиска.
Семантический поиск – это подход, который обеспечивает более тесное смысловое соответствие между текстом поискового запроса и результатами поисковой выдачи на основе анализа намерений пользователя, осуществляющего поиск, контекста его запроса и взаимосвязи между словами.
Понимание взаимосвязи между словами, отношений между сущностями позволяет улучшить качество поиска. Для решения данной задачи используются уже упомянутые нами графы знаний. По данным компании Google, она начала первой использовать графы знаний для реализации семантического поиска в 2012 году. В это время в компании появился лозунг “сущности и контекст, вместо строк ключевых слов”, известный также в короткой его форме “сущности, а не строки”. Граф знаний объединяет большой объем общедоступной информации о различных сущностях и их признаках, свойствах и связях между этими сущностями. В 2013 году в поисковой системе Google появился алгоритм Hummingbird (Колибри), который считается первым поисковым алгоритмом, в котором был реализован семантический поиск, направленный на решение задачи “страницы, соответствующие смыслу, должны быть в приоритете по сравнению со страницами, соответствующими лишь нескольким поисковым словам”. По сути, это означает, что страницы, которые лучше соответствуют контексту и намерениям пользователя, должны ранжироваться выше, чем страницы, которые повторяют ключевые слова без контекста. Для поисковиков это было очень важно, учитывая, что появилось множество недобросовестных методов для поднятия рейтинга страниц путем накачки ключевых слов. В настоящее время графы знаний широко используются технологическими гигантами, которым необходим анализ огромных объемов неупорядоченных данных. Не только Google использует графы знаний. Facebook также использует данную форму организации информации, чтобы отслеживать сети людей и связи между ними, с учетом такой информации, как любимые фильмы и актеры, посещенные мероприятия и т. п.
Netflix так же, как и упомянутые поисковые системы, использует технологию графов знаний для организации информации о своем обширном каталоге контента, устанавливая связи между фильмами, телепередачами, актерами и режиссерами ( рис. 1.22), что помогает предсказывать будущие запросы клиентов.
Рис. 1.22. Граф знаний как основа семантического поиска.
Можно сказать, что семантический поиск – это технология, которая использует модель графа знаний и позволяет системам искусственного интеллекта понимать значение сущностей и связей между ними, давая таким образом возможность увеличить точность поиска и степень его персонализации.
Таким образом, графы знаний – это инструмент сбора информации из разнородных источников и структурирования большого количества взаимосвязанных данных, которые можно исследовать с помощью запросов. Графы знаний используются для создания таких систем, как семантические поисковые системы, рекомендательные системы и разговорные боты.
Несмотря на то, что по массовости применения в решении современных задач ИИ символьный ИИ уступил позиции субсимвольным методам, тем не менее применение символьного ИИ существует и по сей день в современных экспертных системах, таких как, например, платформа ROSS, которая помогает юридическим фирмам в изучении судебных дел, в поисковых системах и других приложениях.
Каждое из направлений ИИ имеет свои сильные и слабые стороны. Многогранность явления ИИ говорит о том, что не существует одного-единственного наилучшего способа для решения широкого спектра задач ИИ. Оптимальные решения могут быть достигнуты на базе комбинирования нескольких подходов. Например, разработки в области символьного ИИ лежат в истоках такого фундаментального направления в области ИИ как NLP (Natural Language Processing, обработка естественного языка), которое в последнее время активно развивается, опираясь на технологии глубокого обучения. Все чаще возникают проекты, в которых речь идет об интеграции символьных и субсимвольных подходов для обеспечения объяснимости ИИ-решений. Прежде чем привести примеры подобных решений, напомним читателю более подробно о сути коннекционистских подходов в создании ИИ.
Коннекционизм
Коннекционизм – от английского слова Connect (соединять) – это направление ИИ, которое исходит из предположения, что ментальные способности человека и, в частности, способность к обучению можно объяснить и имитировать на основе сложноорганизованной сети связанных между собой (соединенных определенным образом) одинаковых относительно простых элементов.
Одним из центральных направлений коннекционизма является моделирование интеллекта с помощью искусственных нейронных сетей, состоящих из нейронов и синапсов (связей между нейронами). Механизм работы искусственных нейронов заимствован из живой природы. Последние были созданы в результате наблюдения за процессами, происходящими в мозге живых организмов. Заметим, что сам термин “нейрон”, используемый в понятии “искусственные нейронные сети” (ИНС), был заимствован из биологии. Представление о том, что развитие и обучение человека базируется на свойствах нейронов мозга устанавливать связи, не ново, согласно данным данная идея была высказана еще в 1932 г. психологом из Колумбийского университета (Нью-Йорк) Эдвардом Торндайком.
Как известно из биологии, нервные клетки при определенном воздействии могут переходить в активированное состояние. Сигналы по нервным волокнам передаются в виде коротких импульсов от клетки к клетке, достигают нервных клеток в мышцах, что приводит к возбуждению мышечных волокон и, соответственно, к движению животного или человека.
Каждая нервная клетка состоит из трех частей: из тела, нескольких ветвистых отростков (дендритов) и протяженного нервного волокна (аксона), длина которого может составлять от нескольких миллиметров до десятков сантиметров (рис. 1.23).
Рис. 1.23. Упрощенная схема передачи сигнала в биологических нейронах
Нервные клетки взаимодействуют между собой в местах стыка (синапсах), где встречаются аксон пресинаптического нейрона и дендрит постсинаптического нейрона. Дендриты являются входными каналами для нервных импульсов, поступающих через аксоны от других нейронов. Эти импульсы могут либо возбуждать (увеличивать), либо подавлять (уменьшать) мембранный потенциал тела нейрона, который со временем возвращается к своему нормальному значению. Если количество возбуждающих импульсов превышает пороговое значение, то нейрон сам генерирует импульс.
Взаимодействующие между собой посредством передачи возбуждений нейроны формируют нейронные сети.
Как будет показано далее, ИНС используют некоторую аналогию с работой живых нервных клеток.
Основополагающей работой, заложившей фундамент для создания искусственных моделей нейронов и нейронных сетей, явилась работа Уоррена С. Мак-Каллока и Вальтера Питтса “Логическое исчисление идей, относящихся к нервной активности”, опубликованная в 1943 г., в которой была предложена модель формального нейрона. Однако прошло более 10 лет, прежде чем появился нейрон Розенблатта, в котором использовалось суммирование входящих сигналов, умноженных на соответствующие числовые значения (синаптические веса) – рис. 1.24.
Несложно проследить сходство схемы, показанной на рис. 1.24, и рисунка 1.24. Модель, прообразом которой является биологический нейрон, представляет собой устройство, имеющее несколько входов (синапсы) и один выход (аксон).
На вход подаются сигналы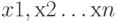
. Каждому входу ставится в соответствие некоторый весовой коэффициент 
.
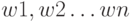Попадая в нейрон, сигналы умножаются на соответствующие веса и складываются между собой (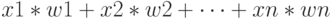
– линейное преобразование). Сложение сигналов, поступающих по синаптическим связям, осуществляется в сумматоре (рис. 1.24).
Известно, что последовательное применение нескольких линейных преобразований эквивалентно одному линейному преобразованию. Если бы модель нейрона ограничивалась одним сумматором, то объединение множества нейронов в сеть было бы эквивалентно одному нейрону. Для того чтобы нарушить это правило, в модель нейрона добавляется нелинейный преобразователь (который реализует нелинейную функцию, которая называется функцией активации).
В рассмотренной модели использовалась пороговая функция активации (ступенчатая функция), которая показана на рис. 1.25 (а). Если суммарный сигнал превышает заданный порог активации, то нейрон возбуждается (активируется) и выдает на выходе 1, иначе выдается 0.
Определенным недостатком (ограниченной гибкостью) модели Уоррена Мак-Каллока являлся именно вид переходной функции (пороговый) – если значение вычисленного суммарного сигнала даже незначительно не достигает заданного порога, то выходной сигнал не формируется.
Такая функция подходит для бинарной классификации, но не подходит, когда для классификации требуется большее число нейронов (количество возможных классов больше двух). То есть если возникает задача, в которой возможно несколько ответов, или нам нужно вероятностное решение, например, с вероятностью 70% это один класс, а с вероятностью 30% – другой.
Впоследствии были реализованы модели нейрона с различными функциями активации. В частности, наиболее широкое использование получила сигмоида – гладкая монотонно возрастающая нелинейная функция, которая ограничена двумя горизонтальными асимптотами, что обеспечивает нормализацию выходного значения нейрона (рис. 1.25 б ) в диапазоне от 0 до 1.
По сути, нейрон представляет собой элементарный вычислитель, характеризующийся входным/ выходным состоянием и функцией активации.
Рис. 1.25. Ступенчатая функция (а) и сигмоидная (б)
На основе элементарных вычислителей, каждый из которых получает сигналы и посылает другим вычислителям, составляются ИНС разной топологии. Самая простая однослойная сеть показана на рис. 1.26.
Рис. 1.26. Однослойная нейронная сеть
Здесь сигналы от входного слоя сразу подаются на выходной слой по связям, каждой из которых устанавливается свой весовой коэффициент.
С помощью подобной сети можно построить работу простейших автоматов. Например, на рис. 1.27 показан автомат (гусеничный робот с тремя датчиками света), реагирующий на положение источника света.
Входные ячейки (фотоэлектрические датчики) реагируют на свет, посылают сигналы на выходные ячейки (нейроны), которые подают сигнал на управление гусеницами робота. Обучить такой автомат разным вариантам движения в зависимости от положения света можно задав весовые коэффициенты, определяющие силу связи между ячейками. В рассмотренном примере задача по обучению робота состояла в необходимости обеспечения движения такой машины за источником света. Для этого были подобраны веса, определяющие силу связи (от 0,45 до 0,99), как показано на рисунке. Еслиположение источника света находится спереди слева от автомата, то активируется вращение правой гусеницы, и наоборот. Несложно представить, что подобная машина будет двигаться за источником света.
Мы рассмотрели простейшую однослойную сеть. Больший интерес представляют многослойные сети. На рис. 1.28 показана многослойная сеть, где каждый нейрон одного слоя посылает сигнал каждому нейрону другого слоя. Данная сеть – это сеть прямого распространения, то есть сеть, в которой сигнал распространяется от входного слоя к выходному в одном направлении.
В показанной на рис. 1.28 сети пять слоев – один входной, три скрытых (промежуточных) и один выходной. Чем больше количество слоев, тем глубже сеть, поэтому и появился термин “глубокое обучение”. Формально при наличии больше одного скрытого слоя уже принято говорить о глубоких нейронных сетях, сети с одним скрытым слоем называют неглубокими (shallow).
Рис. 1.28. Многослойная сеть прямого распространения
Далее поговорим об обучении нейронных сетей. В процессе обучения на вход подается вектор признаков ( рис.1.28), описывающий объект (массив значений), число элементов которого равно числу входных нейронов, на внутренних слоях происходит обработка сигналов, сеть преобразовывает сигнал в выходной слой.
Для того чтобы более наглядно объяснить, как происходит процесс обучения, рассмотрим конкретную задачу распознавания рукописных символов (рис. 1.29).
Как показано на рисунке, изображение рукописного символа (в данном случае цифры 4) разбивается на пикселы, представляется в виде вектора чисел и подается на вход сети.
Если бы все символы были одного размера и начертания, то задача распознавания была бы предельно простой – в том смысле, что сети потребовался бы всего лишь один входной вектор, чтобы запомнить один правильный ответ. Но цифры могут быть напечатаны разными шрифтами, а если мы говорим про рукописные символы, то тут разнообразие еще больше. Все люди пишут числа по-разному – наклон, начертание (все то, что мы называем почерком). И если мы подадим сети, обученной на одном примере, немного измененный входной вектор, соответствующий несколько иному начертанию той же цифры, то правильного ответа уже не получим.
Если необходимо, чтобы сеть классифицировала все многочисленные варианты рукописного написания цифр (например, четверки, показанной на рисунке как числа “4”), то задача состоит в том, чтобы научить сеть способности обобщать признаки на различных входных данных.
Для этого сети нужно продемонстрировать максимально полный набор вариантов написания цифры разными способами, чтобы она “поняла”, какая совокупность признаков позволяет людям относить все разные начертания к одному классу изображений (цифре четыре). Для решения подобной задачи создаются обучающие выборки – данные, по которым обучается сеть. Обучение производится на многочисленных примерах размеченных данных, то есть на базе изображений, в каждом из которых отмечен правильный результат. Подобное обучение называют обучением с учителем или контролируемым обучением. Этот процесс похож на обучение ребенка. Ученику показывают изображение цифры в курсе или написав ее на доске, сообщая при этом правильный ответ. А потом тестируют ученика на знание предмета. Похожая процедура проводится с сетью. Сеть обучают на большом числе примеров по многочисленным вариантам написания каждой цифры, в результате чего подбираются весовые коэффициенты всех связей нейронов, и сеть в результате этой операции приобретает способность распознавать те изображения рукописных цифр, которые ей ранее не были продемонстрированы. После того, как сеть обучена, качество полученной модели проверяют на тестовой выборке. Если тест пройден – модель готова.
На рис. 1.29 условно мы показали процесс распознавания рукописной цифры 4. Затемненные кружки на рисунке отражают процесс возбуждения (активаций) нейронов, приводящих к получению ответа на выходном слое. Темным цветом показана искомая цифра, а светло-серым в выходном слое обозначены нейроны, соответствующие цифрам 1 и 7, что отражает тот факт, что написание этих цифр имеет некоторые схожие признаки с цифрой “4”.
Жизненный цикл нейронной сети, как и любой модели машинного обучения, состоит из двух этапов: обучение (training) и применение (inference). На рис. 1.30 показаны периоды обучения сети: 1 иллюстрирует сеть определенной топологии до начала обучения, 2 показывает процесс обучения. Речь идет о задаче, в которой сеть должна обучиться относить изображения к одному из двух классов – “кошка” и “собака”. По аналогии с предыдущим примером, где речь шла о необходимости продемонстрировать сети все варианты написания цифр, в данном случае сети необходимо продемонстрировать все варианты расположения, все ракурсы, все варианты освещения изображений обоих животных, чтобы сеть могла вычленить общие признаки для распознавания каждого из двух классов на фото. По мере того, как в сеть подаются размеченные изображения (про каждое известно, что там показано – кошка или собака), идет процесс обучения, который состоит в том, чтобы так подобрать весовые коэффициенты, чтобы сеть правильно относила каждое изображение к одному из двух классов. На рисунке на стадии обучения нейроны показаны разных размеров, что условно означает процесс нахождения весовых коэффициентов, которые определяют разную силу связи между соседними нейронами (то есть вес отдельных нейронов). На рис. 1.30 (3-4) условно показан процесс оптимизации сети по производительности: производится удаление избыточных связей в сети – связей, которые определяются малыми весами.
Рис. 1.30. Стадии обучения искусственной нейронной сети. Источник: адаптировано по материалам
На рис. 1.31 представлена более подробная схема, иллюстрирующая стадии обучения и применения нейронной сети с привязкой к ИТ-инфраструктуре. В верхней части диаграммы показана система приема и обработки данных. Левая ветвь показывает процесс обучеия модели.
В случае глубокой нейросети на вход подаются тысячи и более размеченных данных, на которых сеть должна обучиться, чтобы идентифицировать закономерности в данных. Обучение обычно требует больших затрат вычислительных ресурсов, процесс обучения может быть реализован на локальном оборудовании или в облаке.
Обученная и оптимизированная модель передается в систему, где происходит ее применение – сеть распознает новые изображения. Заметим, что обучение сети может являться довольно длительным процессом, а вычисление результатов обученной сетью модели происходит достаточно быстро. Готовая для использования модель может быть размещена в облаке в некотором ЦОДе, локально у заказчика или на периферийном устройстве. В случае периферийного устройства небольшой мощности может быть особенно актуальна стадия оптимизации модели по производительности, о которой мы упомянули ранее.
Выше мы отметили, что для обучения модели на базе нейронных сетей необходимо настроить оптимальные веса для всех связей. Но до сих пор не обсуждали, как это можно сделать.
В сети из нескольких нейронов, как в примере рис. 1.27, весовые коэффициенты можно подобрать вручную. Однако в большей сети необходим автоматический способ поиска оптимальных значений весов (алгоритм обучения). Во время обучения веса, изменяясь на малые величины, приближаются к целевым (оптимальным) значениям.
Важнейшим этапом в развитии нейросетевых подходов явилось появление в середине 80-х годов прошлого века алгоритма обучения, который называется “метод обратного распространения ошибки”. Не вдаваясь в детали, кратко остановимся на сути этого алгоритма.
Обучение нейросети происходит в два этапа – прямого распространения сигнала по сети, после которого вычисляется ошибка предсказания, и распространения ошибки по сети в обратную сторону по тем же самым связям, при котором веса связей сети корректируются таким образом, чтобы повысить успешность решения сетью задачи (уменьшить ошибку). Процесс повторяется до тех пор, пока не будет достигнут желаемый результат.
Поясним процедуру на рассмотренном выше примере с классификацией изображений. На стадии обучения мы представляем нейронной сети изображения вместе с метками (целевыми значениями), которые определяют, что именно изображено на рисунке. Предположим, что на некотором шаге обучения мы предоставили сети изображение кошки. После завершения прямого прохождения данных об изображениичерезсетьмодельформируетвыход, согласно которому изображение на 75% является кошкой. Во время обратного распространения учитывается ошибка, полученная на предыдущем этапе. Веса сети корректируются с учетом ошибки, так, чтобы в следующий раз точность была выше. Корректировка каждого веса осуществляется пропорционально его индивидуальному вкладу в общую ошибку. Поскольку вклад в ошибку от весов в более ранних слоях зависит от вклада весов в более поздних слоях, сигнал ошибки описывается как “обратное распространение ошибки”.
Задача может быть сформулирована как оптимизация некоторой функции потерь, которая зависит от искомых весов. Потери (ошибка) – это разница между текущим предсказанием сети и истинным (определяемым меткой). Веса изменяются на каждой итерации, пока мы не приблизимся к минимуму функции потерь. Цель обучения – минимизировать ошибку или максимизировать точность предсказания, выполняемого моделью.
Символизм и коннекционизм – конкуренция и интеграция
Как мы отметили, символизм и коннекционизм не единственные подходы, на основе которых могут строиться системы искусственного интеллекта. Но прежде, чем упомянуть другие системы, интересно остановиться на сравнении символьного и коннекционистского подходов, поскольку они представляют собой две основные ветви искусственного интеллекта и процесс их развития, конкуренции и взаимо-дополнения в известной степени отражает процесс эволюции ИИ.
Сравнивая упомянутые направления, уместно напомнить понятия “нисходящий” и “восходящий” как два подхода к созданию ИИ. Символьный подход относят к нисходящему (его также иногда называют подход “сверху вниз”), а коннекционистский – к восходящему (или к подходу “снизу вверх”).
В нисходящем подходе познание рассматривается как высокоуровневое явление, которое не зависит от низкоуровневых деталей, то есть абстрагируется от способа реализации механизма работы мозга (в случае природного интеллекта) или принципа действия, конструкции вычислительного устройства (в случае искусственного интеллекта).
Подход “снизу вверх”, или так называемая “восходящая парадигма” – это процесс изучения механизмов, использованных природой, с тем чтобы на их основе создать тот или иной вариант реализации ИИ. Примером последнего подхода является процесс создания искусственных нейронных сетей, которые базировались на изучении нейросетевой структуры мозга животных и человека.
Использование вышеописанных подходов можно проиллюстрировать на разных вариантах построения программы распознавания символов – например, символы можно распознавать на основе описания начертания той или иной буквы, в виде определения совокупности правил: “если буква состоит из трех отрезков, двух длинных и одного короткого, которые расположены таким-то образом, то следовательно – это буква А”. Это символьный или нисходящий подход. В восходящем подходе речь может идти об обучении нейронной сети путем представления ей изображений большой совокупности букв “А”, написанных разными способами, так что сеть сможет вычленить общие признаки для всех вариантов написания буквы и начать ее распознавать.
Исторически символьный подход был первым направлением, на базе которого удалось создать коммерчески успешные системы искусственного интеллекта. Он господствовал примерно с 1950-х по 1980-е годы.
Нисходящие системы плохо справляются с решением задач, включающих большое количество слабых видов взаимодействий, как, например, в системах распознавания образов. Этим объясняется растущее стремление найти альтернативный, более гибкий подход – что стимулировало обращение к коннекционистским моделям.
Для обучения ИНС требуют больших вычислительных ресурсов и памяти, которые было невозможно удовлетворить в период расцвета символьных методов. Позднее, когда появились более производительные компьютеры, исследования коннекционистских сетей “подход снизу вверх” показали значительные перспективы сначала в области распознавания образов, а позднее и во многих других областях. Общая тенденция выразилась в том, что по мере роста вычислительных возможностей коннекционистские методы в существенной мере потеснили символьные.
Этот процесс наглядно иллюстрирует рис. 1.32, на котором показано соотношение числа цитируемых публикаций, принадлежащих к категориям “Коннекционизм” и “Символизм”. Корпус статей “Коннекционизм” включал более 100 тысяч публикаций, собранных на “Web of Science”, а корпус “Символизм” – примерно 65 тысяч публикаций, собранных по профильным ключевым словам.
Рис. 1.32. Соотношение числа цитируемых публикаций “Коннекционизм”/ “Символизм” (логарифмическая шкала). Источник: адаптировано по материалам. Примечание: ONR – Ofice of Naval Research (Управление военно-морских исследований США)
На рис. 1.32 отмечен 1943 год, в котором, как мы упомянули, появилась модель МакКаллока-Питтса.
Согласно данным Британики, первая нейронная сеть появилась в 1954 году, она была разработана Белмонтом Фарли и Уэсли Кларком из Массачусетского технологического института. Сеть была ограничена 128 нейронами и позволяла распознавать простые шаблоны.
Два года спустя (в 1960 году) в Корнеллском университете был продемонстрирован первый нейрокомпьютер – “Марк-1”, который был способен распознавать некоторые буквы английского алфавита. В современной терминологии перцептроны могут быть классифицированы как искусственные нейронные сети с одним скрытым слоем, с пороговой передаточной функцией и с прямым распространением сигнала.
В это же время шло развитие технологий в области символьного ИИ. В частности, на рис. 1.32 отмечен 1965 год – это год, в котором британский философ и логик Джон Алан Робинсон сформулировал правило резолюций – правило вывода, восходящее к методу доказательства теорем через поиск противоречий. Работы ученого были решающими в развитии языка логического программирования Пролог, оказавшего большое влияние на развитие символьного направления.
Следующее событие, отмеченное на временной шкале рис. 1.32, это 1969 год – год, когда Марвин Минский и Сеймур Пейперт написали книгу под названием “Перцептроны”, в которой были отмечены некоторые ограничения перцептронов, публикация способствовала смещению интереса исследователей искусственного интеллекта в область символьных вычислений.
С середины 70-х годов прошлого столетия до начала восьмидесятых наблюдался, как мы уже упомянули, период охлаждения к теме ИИ. Выход из данной зимы искусственного интеллекта произошел на волне развития экспертных систем.
Однако в конце 1980-х и начале 1990-х годов индустрия ИИ испытала ряд финансовых неудач. На рис. 1.32 этот период обозначен как крах рынка LISP машин. В конце 80-х годов рынок специализированных аппаратных средств искусственного интеллекта испытал давление со стороны настольных компьютеров Apple и IBM, которые быстро набирали вычислительную мощность и вскоре сделали неэффективными более дорогие LISP-машины, что привело к закрытию целой индустрии.
1986 г. отмечен как год появления алгоритма обратного распространения ошибки – популярного алгоритма обучения нейронных сетей, в существенной мере способствовавшего распространению нейросетевых технологий. Алгоритм часто связывают с именем Румельхарта, который внес существенный вклад в развитие метода.
С середины 90-х годов нейронные сети привлекают все больший интерес сообщества разработчиков ИИ.
Глубокие нейронные сети позволили получить ранее недостижимые результаты в задачах предсказания, однако они не дают объяснения человеку того, как именно был достигнут тот или иной результат (не являются интерпретируемыми), что ограничивает их применение особенно в таких приложениях, в которых принятие решения является критичным с точки зрения последствий при неверно принятом решении (например, постановка диагноза и выбор метода лечения).
Если логика семантической сети изначально понятна человеку, то с нейронными сетями такую логику проследить невозможно, что демонстрирует рис. 1.33.
Рис. 1.33. Сравнение символьного и коннекционистского подходов. Источник: Марвин Минский 1991 г.
Наличие недостатков и достоинств в нейросетевом и символьном подходах стимулировало исследователей к созданию гибридных решений. Гибридный подход, известный как нейросимвольный ИИ, сочетает в себе черты двух основных стратегий ИИ символьного и коннекционистского (рис. 1.34).
Рис. 1.34. Гибридный нейросимвольный ИИ.
В символьном ИИ (вверху слева) человек-эксперт должен предоставить “базу знаний”, которую ИИ использует для ответа на вопросы. Глубокие сети (вверху справа) обучаются для получения правильных ответов. Гибридное решение использует глубокие сети для того, чтобы генерировать части базы знаний, необходимые для ответа на заданный вопрос, или формируют признаки, использующиеся далее в процессе вывода.
Мы уже говорили, что там, где критичность принятия решения высока, необходимо решение, где человек контролирует ИИ. Те же соображения справедливы в отношении объяснимости ИИ там, где решение критично с точки зрения недопустимости ошибки, там требуется объяснение – как, на основании чего ИИ принял решение.
Объяснимый искусственный интеллект, или XAI (сокращение от Explainable Artificial Intelligence), – одно из относительно молодых и быстро развивающихся направлений в области ИИ, о котором речь еще будет идти в данном курсе.
Эволюционизм
Эволюционизм можно определить как научное направление, в рамках которого разрабатывается совокупность алгоритмов, моделирующих эволюционные процессы (и механизмы их реализации), наблюдаемые в живой природе. Эти механизмы обеспечили возникновение сложнейших живых организмов на Земле, приспособленных к самым разным условиям обитания. Исследование и использование данных механизмов позволило человеку создать искусственные системы, проявляющие способности достижения оптимальных стратегий поведения в разных внешних условиях. Подобно тому как искусственные нейронные сети получили начало на основе изучения работы нейронов в живых организмах, так эволюционные алгоритмы базируются на наблюдаемых в живой природе процессах наследования, мутации и отбора.
Отметим, что идея построения эволюционных алгоритмов ненамного моложе идеи построения искусственных нейронных сетей. Первые попытки использования цифровых компьютерных моделей для изучения процессов естественной эволюции использовались уже с середины 1950-х годов.
В начале 60-х годов прошлого столетия Ганс-Иоахим Бремерманн представил одни из первых попыток применить моделируемую эволюцию для решения задач численной оптимизации, а также разработал некоторые из ранних теорий эволюционных алгоритмов.
В 1967 году Джоном Генри Холландом были разработаны наиболее значимые генетические алгоритмы (подмножество эволюционных алгоритмов), на базовых принципах работы которых мы коротко остановимся.
Генетический алгоритм – это эвристический поисковый алгоритм, который базируется на идеях теории эволюции Дарвина, которая в самом общем плане утверждает, что эволюция обусловлена небольшими вариациями признаков особей, которые усиливаются под воздействием естественного отбора. Особи с полезными признаками имеют больше шансов размножиться и передать эти признаки потомству, чем организмы с вредными признаками.
Генетический алгоритм моделирует процесс естественного отбора, в котором наиболее приспособленные особи отбираются для производства потомства следующего поколения. Эти наиболее приспособленные особи из популяции производят потомство, которое наследует характеристики родителей, и эти характеристики передаются следующему поколению. Данный процесс продолжается при смене поколений (итерационно) и в конце концов приводит к “искомому” поколению с наиболее приспособленными особями. По сути, этот процесс можно рассматривать как итерационный процесс нахождения наилучшего решения задачи.
В самом общем плане итерационный процесс выглядит следующим образом: экспертом выбирается упрощенное прикидочное решение и проверяется, насколько оно удачно. Если оно удовлетворяет условиям, предъявляемым к решению, то задача выполнена, если решение не удовлетворяет требованиям, то оно модифицируется случайным образом и опять проверяется, не удовлетворяет ли требованиям модифицированное решение. При этом если в реальной жизни смена поколений растений и животных – это длительный селективный процесс, то используя генетический алгоритм можно сократить время между поколениями до считанных секунд компьютерных вычислений.
Можно сказать, что генетический алгоритм позволяет заменить процесс моделирования объекта, отвечающего некоторым требованиям, на процесс моделирования эволюции, приводящий к появлению подобного объекта.
Рассмотрим принципы работы генетического алгоритма на упрощенном наглядном примере.
Задача формулируется так, что ее решение может быть представлено в виде вектора генов (генотипа), где каждый ген может быть представлен некоторым объектом (числом или битом). На рис. 1.35 показана схема, поясняющая соотношение понятий ген, хромосома, популяция, используемых в генетическом алгоритме. Подобно тому как в алгоритмах на базе искусственных нейросетей базовый термин “нейрон” заимствован из нейробиологии, в генетических алгоритмах применяется целый ряд терминов, изначально введенных в генетике (популяция, особь, ген, хромосома, генотип).
В проекте было показано, что случайное разрушение до 10% нейронов в обученной сети не влияло на производительность сети – что напоминает свойство мозга человека переносить ограниченный ущерб, нанесенный хирургическим вмешательством или болезнью.
Среди первых применений можно упомянуть использование сети для принятия инвестиционных решений, распознавания рукописных цифр и определение по внешнему виду некоторых видов вооружений на изображениях.
В 1958 году Розенблатт построил электронное устройство, которое должно было имитировать процессы человеческого восприятия, получившее название “Перцептрон”. Проект базировался на развитии идей МакКаллока и Питтса. Перцептрон должен был передавать сигналы от устройства на базе фотоэлементов в блоки электромеханических ячеек памяти, которые оценивали относительную величину электрических сигналов.
Особь (индивидуум) характеризуется набором параметров – фенотипом. Фенотип – это совокупность внешних и внутренних признаков организма, приобретенных в результате индивидуального развития. Фенотип формируется на основе генотипа (совокупность генов) при участии ряда факторов внешней среды.
Гены соединяются в строку, образуя хромосому (решение). Совокупность хромосом дает популяцию, где любая хромосома есть возможное решение рассматриваемой оптимизационной задачи.
Рис. 1.35. Соотношение понятий ген, хромосома, популяция, используемых в генетическом алгоритме
Процесс поиска решения осуществляется в рамках алгоритма, показанного на рис. 1.36.
Рис. 1.36. Блок-схема генетического алгоритма.
На первом этапе осуществляется создание популяции. На этом этапе (как правило, случайным образом) создается множество генотипов начальной популяции. В терминах генетического алгоритма популяция – это множество возможных решений имеющейся задачи (хромосом), которые образуют пространство поиска.
На втором этапе идет оценивание приспособленности особей (хромосом) в популяции. На этом этапе осуществляется вычисление так называемой функции пригодности или фитнес-функции. Фитнес-функция определяет пригодность, приспособленность особи (описываемой хромосомой), то есть ее способность конкурировать с другими особями. Вероятность того, что особь будет выбрана для размножения, зависит от оценки ее приспособленности.
Фитнес-функция принимает на входе текущее потенциальное решение задачи и выдает значение, оценивающее его пригодность.
На следующем шаге идет проверка выполнения условия остановки алгоритма. Алгоритм прекратит исполняться, если найдено решение, удовлетворяющее требуемому критерию качества, если полученное значение больше не улучшается, если исчерпано число отпущенных на задачу поколений или лимит времени на эволюцию.
Если условие остановки не выполнено, то производится отбор хромосом для производства потомков. Идея фазы отбора заключается в том, чтобы отобрать наиболее приспособленных особей (хромосом) и позволить им передать свои гены следующему поколению.
Особи с высокой приспособленностью имеют больше шансов быть отобранными для воспроизводства. Процесс скрещивания показан на рис. 1.37(а). Для каждой пары родителей, подлежащих размножению случайным образом, выбирается точка кроссинговера (точка разрыва). В этой точке обе хромосомы делятся на две части и обмениваются генетическим материалом. На рис. 1.37(а) точка кроссинговера равна 3. Потомство создается путем обмена генами родителей между собой до достижения точки кроссинговера. Новое потомство добавляется в популяцию.
Некоторые из генов образовавшихся потомков могут подвергнуться мутации для поддержания разнообразия в популяции. На рис. 1.37(б) данный процесс проиллюстрирован тем, что некоторые нули заменены на единицы, а единицы на нули. Есть определенная вероятность, что благодаря мутации особь приобретет новое полезное свойство, если это свойство будет вредным, то такая особь будет отсеяна.
Рис. 1.37. Упрощенная схема, поясняющая работу процессов скрещивания и мутации.
Таким образом, для возникновения новых комбинаций генов используются две операции: кроссинговер (скрещивание), позволяющий создать две новые хромосомы потомков путем комбинирования генетического материала пары родителей, а также мутация, которая может вызывать изменения в отдельных хромосомах.
Со временем эволюционные методы стали применять для оптимизации структуры нейросети, так возник термин “нейроэволюция”. Первые нейроэволюционные алгоритмы появились в 1980-х годах.
В самом общем плане концепция нейроэволюции исходит из того, что по мере эволюции человеческий мозг развивался и эволюционировал, обретая способность все лучше решать определенные задачи. Идея нейроэволюции – запустить эволюционный процесс, подобный тому, который привел к развитию нашего мозга, на базе изменения искусственных нейронных сетей с использованием эволюционных алгоритмов.
Нейроэволюция – это метод машинного обучения, который применяет эволюционные алгоритмы для построения искусственных нейронных сетей. Общей целью является такая эволюция искусственных нейронных сетей, которая приводит к решению определенных задач.
Обучение нейросетей с помощью нейроэволюции наиболее эффективно в задачах обучения с подкреплением, таких как поиск оптимальных стратегий в компьютерных играх. В отличие от классических задач машинного обучения, в них удачность стратегии определяется не на каждом этапе игры, а в конце.
Нейроэволюция позволяет найти нейронную сеть, которая оптимизирует свою работу, учитывая вышеописанную обратную связь, без прямой информации о том, что именно она должна делать.
Существуют нейроэволюционные алгоритмы, которые эволюционно изменяют веса связей при заданной топологии сети, а есть алгоритмы, которые помимо эволюции весов также производят эволюцию топологии сети. В качестве примера можно привести эволюцию поведения в компьютерных играх или управление мобильными роботами.
Принципиальная схема нейроэволюции показана на рис. 1.38.
Рис. 1.38. Принципиальная схема нейроэволюции.
На каждой итерации закодированная информация о нейросети в виде генов декодируется в соответствующую нейросеть, которая тестируется на решении целевой задачи. В качестве целевой задачи на рисунке показана некоторая внешняя среда, в которой необходимо выполнять определенные функции для того, чтобы достигать поставленной задачи. Например, речь может идти об участии в игре и, соответственно, необходимости выполнять действия, которые ведут к выигрышу. В процессе тестирования измеряется производительность исследуемой конфигурации нейросети в решении задачи (фитнес-функция). После оценки всех членов текущей популяции, с помощью рассмотренных выше генетических операторов создается новая популяция. Особи с большей фитнес-функцией заменяют особи с меньшей.
Приложения на базе нейроэволюции нашли применение во многих областях, включая обработку изображений, обработку речи, программную инженерию, построение систем кибербезопасности и используются в целом ряде отраслей, таких как здравоохранение, финансы, робототехника и т. п.
Агентный подход
Центральным элементом данного подхода к построению искусственного интеллекта, как следует из его названия, является понятие агента. Согласно, “агент – это любая сущность физическая или виртуальная, которая воспринимает свое окружение через датчики и действует на это окружение через исполнительные механизмы”.
Под агентом могут подразумеваться разные сущности (программа, робот, человек). Агенты могут действовать в реальном мире (роботы), в виртуальном (персонаж игры), воздействовать на внешний мир из виртуального – чат-боты и другие программные агенты, поддерживающие решения конкретных людей.
Тенденции в разработке программного обеспечения последних лет показывают устойчивое движение в сторону поддержки автономных, рациональных агентов. Для создания интеллектуальных агентов могут использоваться методы машинного обучения, символьный, эволюционный, нейросетевой и гибридные подходы.
Алгоритмы машинного обучения позволяют агенту адекватно реагировать на изменения среды, совершенствовать правила поведения или приобретать интеллектуальное поведение.
Агенты можно классифицировать по степени их интеллектуальности, по способности рассуждать. Самые простые агенты – это реактивные агенты, они имеют простейший тип поведения, основываются на минимальном объеме информации и простых правилах: “ситуация-действие”, “запрос-ответ”.
Так называемые делиберативные агенты используют некоторые логические рассуждения и/или возможности планирования (1.39).
Агенты можно классифицировать по месту, где они выполняют свой код: статические агенты работают на выделенном сетевом узле, мобильные агенты могут перемещать свой код c одного компьютера на другой между узлами сети.
По поведению агенты можно разделить на пассивные (не имеют конкретных целей, могут реагировать на внешние раздражители, но сами не будут инициировать никаких действий) и активные (имеют определенные цели, которые они преследуют). Используется также термин “когнитивные агенты” – агенты, которые предполагают сложное планирование и рассуждения.
Агенты часто работают не поодиночке, а в рамках некоторой многоагентной системы. Многоагентная система – это слабо связанная сеть агентов, решающих некоторые задачи. Агенты работают вместе, чтобы найти ответы на вопросы, которые выходят за рамки индивидуальных возможностей или знаний каждого агента.
Многоагентные системы можно классифицировать по типу сотрудничества агентов (рис. 1.40).
Многоагентная система может иметь независимых агентов – каждый агент преследует свои собственные цели. В такой системе агенты могут не сотрудничать, но также возможен вариант, когда сотрудничество не запланировано, но может возникать спонтанно – в этом случае такие системы называют системами с эмерджентным сотрудничеством.
Многоагентные системы называются сотрудничающими, если у ее агентов есть общие цели, при этом ее агенты могут взаимодействовать между собой, а могут не взаимодействовать.
Сотрудничество внутри многоагентной системы может быть явно спроектировано разработчиком и может реализоваться путем адаптации, когда сотрудничество отдельных агентов развивается в ходе какого-то эволюционного процесса.
Многоагентный подход обеспечивает устойчивость и масштабируемость системы. За счет того, что ответственность за выполнение общей задачи распределена между большим числом агентов, система может переносить сбои одного или нескольких агентов.
Такие характеристики многоагентных систем, как гибкость и надежность, делают их эффективным подходом для решения многих сложных задач. Подобная задача делится на множество мелких простых подзадач, которые распределяются между агентами. Потребление ресурсов в такой системе оптимизируется между несколькими агентами, что часто приводит к менее затратному решению по сравнению с подходом, при котором вся задача выполняется одним агентом.
Возможны разные типы многоагентных систем по способу организации агентов. В качестве примера на рис. 1.41 показана иерархическая и коалиционная организация. В первом случае отдельные агенты организованы в древовидную структуру, часто используемую при управлении сотрудниками в компании. Агенты, находящиеся выше по дереву, имеют более высокий уровень осведомленности. Данные, получаемые агентами нижнего уровня, передаются вверх, а управленческие распоряжения вниз. В коалиционном типе организации агенты группируются в соответствии со своими целями в группы агентов, имеющих схожие цели.
Из конкретных примеров можно привести проект компании Waymo, которая создала среду многоагентного моделирования Carcraft для тестирования алгоритмов беспилотных автомобилей, где имитируется дорожное взаимодействие между водителями-людьми, пешеходами и самоуправляемыми автомобилями.
-
Add a note